Ein Thema mit Hilfe von Schätzungen zu erkunden bedeutet, dass viele Schätzungen mit verschiedensten Annahmen aus unterschiedlichen Blickwinkeln durchgeführt werden müssen. Je mehr Ergebnisse auf diesem Weg gewonnen werden, desto unübersichtlicher werden die Ergebnisse. Das ist vergleichbar mit der Vermessung eines unbekannten Landes. Bei der Vermessung eines unbekannten Landes wird gedanklich ein Netz aus Dreiecken über das Land gelegt. Es werden Winkel und Himmelsrichtungen gemessen und es entstehen Tabellen mit geodätischen Rohdaten. Diese geodätischen Rohdaten sind allerdings für einen Wanderer, der sich in dem vermessenen Land orientieren möchte, völlig nutzlos. Erst dann, wenn die geodätischen Rohdaten zu Landkarten zusammengefügt werden, werden diese Daten für Wanderer nutzbar.
Genau so ist es, wenn eine unbekannte Situation durch Beobachtungen, Messungen und Schätzungen erkundet werden soll. Aus den Schätzungen ergeben sich viele Zahlen, Diagramme und Formeln, die häufig aufeinander aufbauen. Während in der Geodäsie lediglich ein Raum mit drei Dimensionen vermessen wird, findet die Erkundung einer unbekannten Situation durch Schätzungen in einem multidimensionalen Bereich statt. Jede Variable, jede Annahme ist eine Dimension, die variiert werden kann. Daraus ergibt sich keine simple Landkarte, die sich einfach darstellen lässt. Es handelt sich vielmehr um eine Mannigfaltigkeit, die über Fixpunkte Stückweise erfasst wird. Jede einzelne Schätzung ist ein Fixpunkt, bei dem nicht nur das Endergebnis wichtig ist, sondern auch die Schlusskette aller getroffenen Annahmen.

Mit Mannigfaltigkeit meine ich hier den Sachverhalt, dass ein einzelner Fixpunkt, der durch eine Schätzung ermittelt wurde, für sich allein betrachtet in sich geschlossen erscheint. Bei globaler Betrachtung der Situation wird aber deutlich, dass die Ergebnisse einer einzigen Schätzung verstärkt von der Realität abweichen können, je globaler die Situation betrachtet wird. Spätestens dann werden weitere Schätzungen erforderlich und es ergeben sich weitere Fixpunkte.

Zur Erfassung dieser Mannigfaltigkeit haben sich meiner Erfahrung nach Formelsammlungen und Tabellenwerke am besten bewährt. Formelsammlungen und Tabellenwerke müssen dabei ausführliche Quellenangaben beinhalten. Ich möchte an dieser Stelle die Wichtigkeit von Quellenangaben betonen. Ohne Quellenangaben sind Tabellenwerke und Formelsammlungen etwas, über dass man sich später ärgert. Quellenangaben ermöglichen einem Leser die weitere Recherche und ein tieferes Verständnis, weshalb sie so wertvoll sind.

In Tabellenwerken finden sich eine Auswahl weniger Zahlen, die in der Praxis besonders häufig vorkommen. Diese ausgewählten Zahlen sorgen für eine grobe Orientierung. Formelsammlungen bieten eine Auswahl an Gleichungen, die sich in der Praxis als besonders nützlich erwiesen haben. Mit diesen Gleichungen kann man dann bei der Erweiterung der Schätzungen weitere Zahlen für konkrete Anwendungsfälle berechnen, oder Extremwerte ermitteln.

Ich möchte diesen Sachverhalt an einem konkreten Beispiel deutlich machen. In diesem Beispiel geht es um den Heizenergiebedarf von Gebäuden. Als Beispiel soll folgende Graphik aus der Energieeinsparverordnung dienen. Diese Graphik zeigt typische jährliche, auf die Wohnfläche bezogene Energieverbrauchskennwerte von Gebäuden.

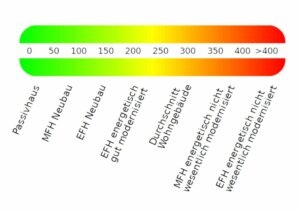
Typische wohnflächenbezogene Energieverbrauchskennwerte von Gebäuden in Deutschland laut Energieeinsparverordnung 2007 in kWh/(m² a). EFH: Einfamilienhaus. MFH: Mehrfamilienhaus. Quelle: Bundesgesetzblatt Jahrgang 2007 Teil I Nr. 34, ausgegeben zu Bonn am 26. Juli 2007. Seite 1553

In diesem Diagramm wird der Energieverbrauch in Kilowattstunden pro Quadratmeter Wohnfläche pro Jahr angegeben. Diese Werte sind nützlich, wenn der Heizenergiebedarf eines Gebäudes schnell und grob überschlagen werden soll. Diese Werte berücksichtigen allerdings keine baulichen Besonderheiten eines Gebäudes, wie zum Beispiel besonders dünne oder dicke Wände oder besondere Gebäudeöffnungen oder die Lage des Gebäudes. Soll der Energieverbrauch des Gebäudes genauer bestimmt werden, kann dieser mit Hilfe der Gleichungen berechnet werden, die in der DIN 4108 angegeben sind. Allerdings sind auch diese Gleichungen nur dazu da, um Näherungswerte unter Standardbedingungen zu ermitteln. Wenn es sich bei dem Gebäude allerdings um eine alte Mühle handelt, die in einem tiefen schattigen Tal an einem Mühlbach liegt, sind auch diese Gleichungen nur bedingt aussagekräftig. Trotzdem sind die Gleichungen der
DIN 4108 ein nützliches Werkzeug, um den Heizenergiebedarf von Gebäuden zu bewerten und abzuschätzen.

An diesem Beispiel sollte deutlich werden, wie dokumentierte Zahlenwerte und Gleichungen einen Überblick über ein komplexes Thema bieten können. Aus diesem Grund ist es meiner Ansicht nach ratsam, parallel zur Durchführung von Beobachtungen, Messungen und Schätzungen, die gewonnen Ergebnisse in Formelsammlungen und Tabellen zu dokumentieren. Sobald eine Schätzung erweitert wird und an Komplexität zunimmt, ist das Anfertigen von Tabellen und Formelsammlungen zwingend notwendig. Auch die Verwendung von Tabellenkalkulationsprogrammen ist bei der Durchführung von Schätzungen nützlich, weil auf diese Weise quantitative Änderungen in den Annahmen und Korrekturen schnell in die Schätzung aufgenommen werden können. Dadurch werden auch alle Folgeergebnisse neu berechnet, was sehr viel Aufwand spart.